| ENG RUS | Timus Online Judge |
Ural Regional School Programming Contest 2010
Contest is over
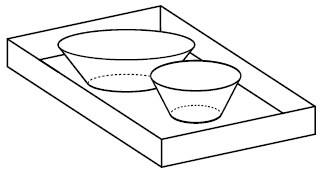
I. Tray 2Time limit: 1.0 second Memory limit: 64 MB One of the organizers of the Ural Regional School Programming Contest came to the university cafeteria to have
lunch. He took a soup and a main course and tried to arrange them on a small rectangular tray, which was not so
easy. “Oops, that's a problem,” he thought. “Oh, yes, that's a problem! A nice problem for the contest!”
The Ural State University's cafeteria has trays with a rectangular a × b bottom and vertical
borders of height d. Plates have the shape of a truncated cone. All the plates in the cafeteria have the
same height h. The organizer wants to put the plates on the tray so that their bottoms adjoin the bottom
of the tray completely. Can he do it?
 InputThe first line contains the integers a, b, and d separated with a space. Each of the
following lines describes one of the plates and contains two integers. The former integer is the radius of
the plate's bottom and the latter integer is the radius of the circle formed by the edge of the plate.
The second radius is greater than the first one. The last line contains the height h of the plates.
All the input integers are positive and do not exceed 1000.
OutputOutput “YES” if the plates can be arranged on the tray and “NO” otherwise. Samples
Problem Author: Sofia Tekhazheva Problem Source: Ural Regional School Programming Contest 2010 |
