| ENG RUS | Timus Online Judge |
1202. Путешествие по прямоугольникамОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ На бесконечном листе клетчатой бумаги заданы оси координат. Единицей измерения в этой системе координат является длина стороны квадратной клетки. На листе бумаги находятся N прямоугольников. Их стороны параллельны осям координат и проходят по границам клеток. Обозначим координаты левого нижнего угла i-го прямоугольника как (xi, yi), а координаты правого верхнего угла как (xi, yi). Выполняются следующие соотношения: x1 = 0, y1 = 0 xi = xi + 1 2 ≤ xi − xi ≤ 100 2 ≤ yi − yi ≤ 100 Если прямоугольники с номерами i и i + 1 соприкасаются, их общая граница исчезает: 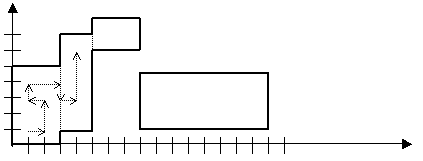 Путешественник начинает свой путь в точке с координатами (1, 1), которая, как следует из соотношений, приведённых выше, обязательно лежит в первом прямоугольнике. Путешественник идёт строго по границам клеток. Ему не разрешено проходить по границам прямоугольников, поэтому путешественник может перейти из одного прямоугольника в другой только через их исчезнувшую общую границу. Пример возможного начала пути приведён на рисунке. Цель путешественника — точка (xn − 1, yn − 1), очевидно, находящаяся внутри последнего прямоугольника. Исходные данныеВ первой строке находится положительное число n, 0 < n < 100 000 — количество прямоугольников на плоскости. Затем идут n строк, каждая из которых содержит четыре целых числа xi, yi, xi, yi, разделённых пробелами и удовлетворяющих описанным выше соотношениям. РезультатВыведите длину (единица измерения — сторона клетки) кратчайшего пути из точки (1, 1) в точку (xn − 1, yn − 1) или число −1, если такого пути не существует (пример такой ситуации показан на рисунке). Пример
Автор задачи: Леонид Волков Источник задачи: Соревнование команд УрГУ, март 2002 Метки: нет |
