| ENG RUS | Timus Online Judge |
1318. ЛогарифмОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Дан набор чисел A, состоящий из N неупорядоченных 128-битных чисел. Необходимо вычислить функцию 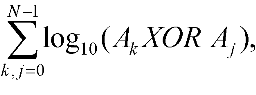 Ak – k-е число из исходного набора, log10X – целая часть десятичного логарифма числа X. Будем считать, что log100 = 0. Исходные данныеВ первой строке находится число N ≤ 5000. Далее в следующих N строках записаны 128-битные числа Ak, представленные четверками чисел (a1k, a2k, a3k, a4k), каждое из которых находится в интервале от 0 до 232-1. Из этой четверки 128-битное число Ak получается по формуле Ak = 296a1k + 264a2k + 232a3k + a4k. РезультатВыведите значение функции для данного набора. Пример
Автор задачи: Идея – Никита Шамгунов, подготовка – Никита Шамгунов, Антон Ботов Источник задачи: VIII Командный студенческий чемпионат Урала по программированию. Екатеринбург, 11-16 марта 2004 г. Метки: нет |
