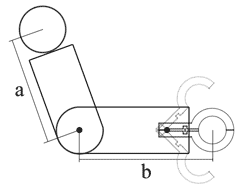Рука робота устроена по тому же принципу, что и человеческая. Она состоит из плеча и предплечья. Плечевой сегмент закреплён в плечевом суставе так, что может вращаться в этом суставе в любом направлении. Предплечевой сегмент соединяется с плечевым в локтевом суставе. Предплечье может поворачиваться относительно плеча вокруг оси, проходящей через локтевой сустав и перпендикулярной плечу и предплечью. Угол сгиба руки в локтевом суставе не может быть острым. На конце предплечевого сегмента имеется клешня, состоящая из двух одинаковых частей, которые могут смыкаться и размыкаться. В момент, когда клешня полностью сомкнута, она может держать цилиндр единичного диаметра. В таком положении ось цилиндра будет параллельна оси локтевого сустава.

Робот увидел рядом с собой цилиндрический поручень бесконечной длины и единичного диаметра. Он разомкнул клешню и хочет схватиться за этот поручень, но так, чтобы клешня могла полностью сомкнуться. Определите, какое положение должна принять рука робота, чтобы он мог сделать это.

В первой строке указаны числа a и b — длина соответственно плечевого и предплечевого сегментов руки. Во второй и третьей строках указаны координаты двух различных точек, лежащих на оси поручня. Координаты даны в системе отсчёта с центром в плечевом суставе. Поручень не проходит сквозь плечевой сустав. Все числа целые и не превышают по модулю 100; a, b ≥ 4. Толщиной плеча и предплечья следует пренебречь.

Если не существует положения руки робота, при которой он может сомкнуть клешню на поручне, выведите «No solution.» Иначе выведите координаты локтевого сустава и угол сгиба руки в нём в радианах с максимально возможной точностью. Значение угла должно лежать в диапазоне [π/2, π]. Если существует несколько вариантов решения, выведите любой из них.