| ENG RUS | Timus Online Judge |
1887. Карта постоянного пассажираОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Компания Oceanic Airlines представила новый продукт для своих
постоянных клиентов — карту постоянного пассажира. Если при
регистрации на рейс пассажир предъявит эту карту, то на неё будет
зачислена десятая часть миль, которые пролетит самолёт. В
дальнейшем накопленные мили можно будет обменять на билет на
другой рейс компании Oceanic Airlines, сэкономив значительную сумму
денег. Например, купив билеты на рейсы Екатеринбург-Франкфурт,
Франкфурт-Нью-Йорк и Нью-Йорк-Орландо, впоследствии можно будет бесплатно получить
билет на рейс Екатеринбург-Варшава. У каждой карты постоянного пассажира есть уникальный номер, состоящий из n + 1 десятичной цифры.
Первые n цифр могут быть произвольными (обозначим их x1, …,
xn). Последняя цифра является проверочной и вычисляется по формуле 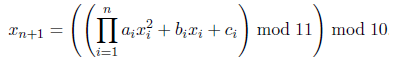 где (p mod q) обозначает операцию взятия остатка от деления p на q, результат
которой — такое целое число r, что Номера карт генерируются следующим алгоритмом: каждой из первых n цифр
равновероятно и независимо друг от друга задаётся значение от 0 до 9,
после чего значение последней цифры
вычисляется по
приведённой формуле. Руководство авиакомпании решило, что последние цифры первых
десяти проданных карт должны быть попарно различными. Сколько в среднем
номеров карт придётся сгенерировать описанным алгоритмом, чтобы получить среди них
десять номеров с попарно различными последними цифрами? Исходные данныеВ первой строке задано целое число n (2 ≤ n ≤ 25),
во второй строке записаны целые числа a1, …, an,
в третьей строке записаны целые числа b1, …, bn,
в четвёртой строке записаны целые числа c1, …, cn
(0 ≤ ai, bi, ci ≤ 9). РезультатВыведите единственное вещественное число — ожидаемое количество раз,
которое придётся сгенерировать первые n цифр карты, чтобы получить десять
карт с различными последними цифрами. Абсолютная или относительная
погрешность ответа не должна превосходить 10−6. Если
не существует десяти номеров карт с попарно различными последними цифрами, выведите «-1». Примеры
Автор задачи: Евгений Курпилянский Источник задачи: NEERC 2011, Четвертьфинал Восточного подрегиона |
