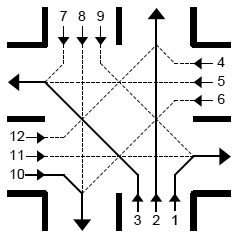Перекрёсток проспекта Ленина и улицы 8 Марта находится в самом центре Екатеринбурга, поэтому неудивительно, что пробки на нём стали обычным делом. В этой задаче вам предстоит помочь городу с разгрузкой перекрёстка.

Приближаясь к перекрёстку с одной из четырёх сторон, машины делятся на три потока: поворачивающие налево, направо и едущие прямо. Каждый из 12 потоков регулируется отдельным светофором. Они действуют согласованно и могут раз в минуту одновременно менять свои состояния. Но их сигналы не должны противоречить друг другу. Это означает, что потоки машин, проезжая перекрёсток, согласно сигналам светофоров, не должны пересекаться.

Например, если разрешено прямое движение в северном направлении, то с западной стороны перекрёстка прямое движение должно быть запрещено, так как оно небезопасно. Однако правый поворот с западной стороны может быть разрешён. Два автомобильных потока считаются пересекающимися, если они имеют одинаковое конечное направление движения или если их траектории пересекаются при переезде через перекрёсток. На иллюстрации потоки, выделенные жирным (под номерами 1, 2, 3 и 10), не пересекаются друг с другом, а каждый из остальных потоков пересекает хотя бы один из выделенных жирным.

Предположим, что известны 12 целых чисел n_i — количество автомобилей, желающих проехать перекрёсток в каждом из направлений (направления нумеруются числами от 1 до 12, как показано на рисунке), а также 12 скоростей пересечения перекрёстка v_i — количество автомобилей, которые за минуту успели бы проехать перекрёсток в данном направлении, если бы движение было разрешено. Предположим также, что новые автомобили не приезжают. Вам необходимо, управляя светофорами в течение 10 минут, максимально разгрузить перекрёсток. Требуется добиться того, чтобы максимальное количество автомобилей, оставшихся в одном из 12 потоков, было как можно меньше.

В первой строке записаны 12 целых чисел n_i, 0 ≤ n_i ≤ 1000. Во второй строке записаны 12 целых чисел v_i, 1 ≤ v_i ≤ 1000.

Выведите количество автомобилей, оставшихся в том из 12 потоков, который через 10 минут будет самым загруженным, при оптимальном управлении светофорами.

Больше всего машин направляется с запада на восток (поток номер 11), и им необходимо разрешить движение в течение всех десяти минут. Первые четыре минуты можно разрешить движение всем машинам с востока (4 и 5), так как никто из них не поворачивает на юг. Оставшиеся шесть минут стоит пропустить поток с севера на запад (7).