| ENG RUS | Timus Online Judge |
Чемпионат Урала 2009
Соревнование завершено
H. Секрет ГипножабыОграничение времени: 5.0 секунды Ограничение памяти: 64 МБ  Все любят Гипножабу! Её шоу — одно из самых популярных на телевидении.
Правда, после его просмотра люди не могут вспомнить, о чём оно было и даже
что они всё это время делали. И всё же многочисленным фанам Гипножабы
это не мешает испытывать воистину положительные эмоции от любимого зрелища. Профессор Фарнсворт для изучения интереснейших свойств Гипножабы
сконструировал специальный прибор, улавливающий и сканирующий её волны.
Ему удалось выяснить, что в каждый момент времени её глаза могут находиться в
одном из n состояний. Для простоты профессор обозначил эти состояния числами
0, 1, …, n−1. Состояния глаз меняются по одному из линейных законов,
для каждого из которых профессор смог вычислить формулу.
Всего получилось m законов, каждый из них можно задать 5 целыми числами:
s0, t0, Δs, Δt, k.
Когда Гипножаба «работает» по такому
закону, её левый глаз принимает состояние si,
а правый — ti
последовательно для всех целых i от 0 до k−1, где si = (s0 + i Δs) mod n, ti = (t0 + i Δt) mod n. После нескольких недель исследований Фарнсворт понял, что с помощью волн
Гипножабы можно узнать многие секреты устройства Вселенной. Например,
Гипножаба способна видеть тёмную материю и получать информацию из чёрных
дыр. Для того чтобы научиться видеть так же как Гипножаба, профессор собрал
новый прибор, который эмулирует «гипнозрение»: каждый из четырёх его
окуляров может принимать одно из n состояний, которые меняются по линейным
законам.
Фарнсворт провёл серию экспериментов и для каждого из них построил диаграмму,
на которой для всех возможных состояний прибора отметил, могут ли глаза
Гипножабы принимать состояния, похожие на состояния окуляров.
Помогите профессору автоматизировать этот процесс.
Один эксперимент описывается 9 целыми числами:
a0, b0, c0, d0,
Δa, Δb, Δc, Δd, q.
Для всех целых значений j от 0 до q−1 окуляры последовательно
принимают состояния
aj = (a0 + j Δa) mod n, bj = (b0 + j Δb) mod n, cj = (c0 + j Δc) mod n, dj = (d0 + j Δd) mod n. Для каждого состояния прибора (aj, bj,
cj, dj) требуется определить,
могут ли глаза Гипножабы принимать такое состояние
(si, ti), что
min(aj, bj) ≤
si ≤
max(aj, bj), min(cj, dj) ≤ ti ≤ max(cj, dj). Исходные данныеВ первой строке записаны целые числа n и m — количество состояний
глаз Гипножабы и количество законов их поведения
(1 ≤ n ≤ 5000, 1 ≤ m ≤ 1000).
В каждой из следующих m строк записаны целые числа
s0, t0, Δs, Δt, k,
задающие закон изменения состояний глаз
(0 ≤ s0, t0, |Δs|,
|Δt| ≤ n−1; 1 ≤ k ≤ 567).
В следующей строке записано целое число p — количество экспериментов
(1 ≤ p ≤ 345).
В каждой из следующих p строк записаны целые числа
a0, b0, c0, d0,
Δa, Δb, Δc, Δd, q,
описывающие эксперимент
(0 ≤ a0, b0, c0,
d0, |Δa|, |Δb|, |Δc|,
|Δd| ≤ n−1; 1 ≤ q ≤ 345).
РезультатВыведите p строк: по одной на каждый эксперимент.
Для одного эксперимента вычислите его результат —
набор чисел xj для j = 0, 1, …, q−1,
где xj = 1, если глаза Гипножабы могут принимать подходящее состояние
для соответствующего состояния прибора, и xj = 0 в противном случае.
Если q ≤ 20, выведите все xj подряд без пробелов.
Если q > 20, выведите одно число, равное
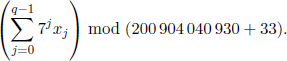 Пример
Автор задачи: Дмитрий Иванков Источник задачи: XIII чемпионат Урала по спортивному программированию, 4 апреля 2009 г. |
