| ENG RUS | Timus Online Judge |
Ural SU contest. Petrozavodsk training camp. Summer 2010
Соревнование завершено
I. Охота на зайцев 2Ограничение времени: 4.0 секунды Ограничение памяти: 64 МБ Хороший охотник убивает одним выстрелом двух зайцев. Но чтобы стать лучшим охотником в мире, вам нужно
научиться убивать максимально возможное количество зайцев одним выстрелом. В этом вам поможет программа
Rabbit Hunt 2. Программа считает всех зайцев точками на плоскости. Ей на вход подаются координаты
n зайцев, после чего она генерирует q возможных вариантов выстрела и выбирает из них тот, который
убьёт наибольшее количество зайцев. Выстрел задаётся точкой, где должен стоять охотник, и направляющим вектором
луча, по которому летит пуля. Считается, что выстрел убивает всех зайцев, лежащих на этом луче, в том числе зайца,
расположенного в той же точке, что и охотник. Генератор позиций использует числа ax, bx, ay, by, avx, bvx, avy, bvy.
Координаты охотника в первой позиции — (x1, y1), а направление первого выстрела — (vx1, vy1).
Координаты охотника и направляющий вектор для i-го выстрела (i > 1) вычисляются по формулам: 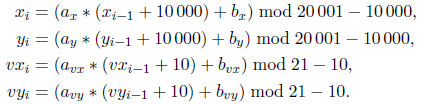 Проблема в том, что программы Rabbit Hunt 2 ещё не существует. Вам предстоит её написать. Исходные данныеВ первой строке записано целое число n (1 ≤ n ≤ 10 000) — количество зайцев. В каждой из следующих
n строк через пробел записаны координаты очередного зайца. Координаты — целые числа,
по модулю не превосходящие 10 000. Никакие два зайца не расположены в одной точке.
В следующей строке записано целое число q (1 ≤ q ≤ 106) — количество генерируемых позиций.
В следующей строке через пробел записаны целые числа x1, y1, vx1, vy1 РезультатВыведите через пробел два числа — номер позиции, для которой количество убитых зайцев будет максимально, и это количество.
Если таких позиций несколько, выведите позицию с наибольшим номером. Пример
Автор задачи: Алексей Самсонов Источник задачи: Ural SU Contest. Petrozavodsk Summer Session, August 2010 |
