| ENG RUS | Timus Online Judge |
USU Junior Contest October'2001
Contest is over
A. Piecewise Constant FunctionTime limit: 0.5 second Memory limit: 64 MB 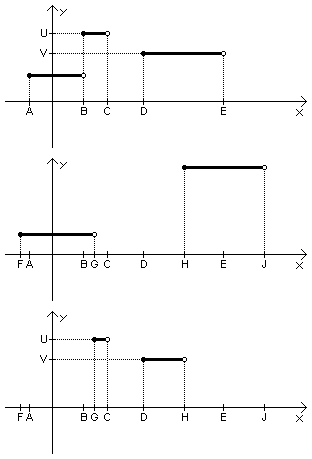 SKB Kontur has been developing a new SKB Kontur Framework for the last three months. One of the latest wrinkles is that data will be presented with the help of piecewise constant functions. Your team is to implement an operation of "subsettraction" of the functions. A function is called piecewise constant if its domain can be divided into intervals and the function is constant on each interval. We also assume that the function value at the left-end point of each interval of constancy is equal to its value on the interval. In fig.1 there is a piecewise constant function with three intervals of constancy. Note that the function value at the point B is U and at the points C, E and on the interval (C,D) - the function value is not defined. A result of the subsettraction operation of two piecewise constant functions
F1 @ F2 is a piecewise constant
function F defined as follows:
In Fig.3 there is the result of the operation of the subsettraction of the two functions from Fig.1 and Fig.2. Inputcontains two lines of the same format. Each line characterizes one piecewise
constant function. A line begins with an integer N (1 ≤ N ≤ 15000). Then characterizations of constancy intervals follow in the
ascending order with respect to their left ends. Each interval is given by three integer
numbers A, B, Y (|A| < 32000, |B|
< 32000, |Y| ≤ 100, A < B), where A
is the left end of an interval, B is the right end of an interval and
Y is the function value on the interval. It's known that that no two
intervals from one line intersect. If two intervals are adjacent, the function values on the intervals are different. Outputcontains one line of the same format (see the input specification).
This line should describe a result of the operation of subsettraction of the two input
piecewise constant functions. Sample
Problem Author: Oleg Kaz Problem Source: USU Open Collegiate Programming Contest October'2001 Junior Session |
