| ENG RUS | Timus Online Judge |
1334. CheckersTime limit: 1.0 second Memory limit: 64 MB Taking the front staircase, which to my memory was used only once when the most august personage from Africa came to visit, I descended into the limitless vestibule decorated with a multi-century accumulation of layers of architectural excesses, and peered into the gatehouse window. Two Maxwell macro-demons were oscillating about in its phosphorescent gloom. They were playing at the most stochastic of all games — pitch-and-toss. They occupied all their free time with this diversion. Looking more like poliomyelitis virus colonies under an electron microscope than anything else, they were huge, indescribably inept, lethargic, and dressed in worn liveries. As befit Maxwell demons, they opened and closed doors throughout all their life. They were experienced, well-trained exemplars, but one of them, the one in charge of the exit door, had reached retirement age, which was comparable to the age of the galaxy, and now and then reverted into second childhood, malfunctioning ignominiously. Thereupon, someone from Technical Maintenance would put on a driving suit, enter the gatehouse with its argon atmosphere, and bring the oldster back to reality.
Following instructions, I cast a spell on both of them, that is, I crossed the information channels and locked the input-output peripherals to myself. The demons did not react, being otherwise absorbed. One was winning, and, correspondingly, the other was losing, which greatly disturbed them, since it upset the statistical equilibrium. The fact is that pennies matching is not stochastic enough. Sasha is lost in thoughts what game may be better. Maybe it is stochastic checkers? This is a very simple game. Demons in turns put checkers of two colors on the black cells of the chess field. Loses that player, after whose move one of the opponents gets the opportunity to fell the checker. 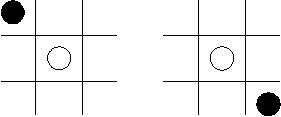 Checker A may be felled by checker B if checkers A and B are of different color and a cell, on which B comes after "jumping over" checker A, is free. You need to determine what move the given set of stochastic checkers was lost on. InputThere is a description of 32 stochastic checkers’ moves in traditional chess notation in the input. Moves of white pieces are in lines with odd numbers, and moves of black pieces are in lines with even numbers. OutputOutput the number of move on which a set was lost, or the word "Draw", if a set was not lost by either demon. Sample
Problem Author: Den Raskovalov Problem Source: The 10th Collegiate Programming Contest of the High School Pupils of the Sverdlovsk Region (October 16, 2004) Tags: none |
