| ENG RUS | Timus Online Judge |
2016. Magic and ScienceTime limit: 1.0 second Memory limit: 64 MB Scientists who specialize in witchcraft have recently discovered
a new elementary particle called a magion.
Studying the laws of magions’ movement, a group of three scientists
conducts the following experiment. The scientists created positvie homogeneous aura in the laboratory.
The force of interaction with this aura has constant value and
is up-directed.
If no other force affects the magion, the aura will make the magion
move with constant acceleration (0,0,a). A magion with initial speed equal to zero is placed to the point
M1 = (0,0,0). At the beginning the first scientist creates a bundle of mana
at the point O1. Magion is immediately affected by the bundle
and while the latter exists it will be at the distance O1M1
from the point O1. As a result, the magion starts moving up
along the arc of the circle omega1 with the center at O1. At some moment the first scientist annihilates the bundle of mana at O1,
and the second scientist at the same time creates his own bundle
at the point O2. The moment for this is being chosen in the following way.
The position of the point O2 is being chosen so that the point M2
is uniquely determined and does not coincide with the point M1.
Affected by the second bundle, the magion continues its movement
along the circle omega2 with the center at the point O2 and
with the point M2 on it. 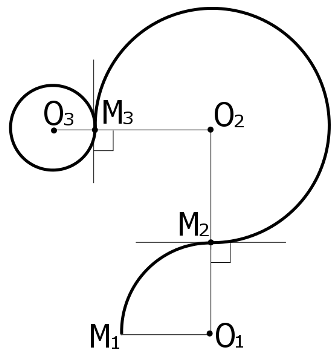 After that the procedure is repeated,
i. e. the second scientist annihilates his bundle of mana, and
the third one creates his own bundle at the point O3.
The magion, being at this moment at the point M3, now starts moving
along the circle omega3 with the center in O3.
The third scientist waits until the magion finishes the full circle
along omega3 and returns to the point M3. This moment is considered
the end of the experiment. All scientists choose moments and points to create bundles of mana
so that the point Mi does not coincide neither with Mi−1 nor Oi,
and the distance from Oi to any point of the circle omegai−1,
other than Mi, is strictly greater than OiMi.
Apart from that, at every moment except the initial one the scientists
don’t allow the magion’s speed to be zero. At any moment of time the magion is affected by exactly two forces:
the force of interaction with the bundle of mana and
the force of interaction with the aura. The first one is always directed
perpendicularly to the magion’s path of motion and
therefore doesn’t affect the absolute value of magion’s speed. Knowing the coordinates of the points Oi and the value of
the acceleration a being imparted to the magion by the positive aura,
will you be able to define the overall length of the magion’s path segments
where its speed is not less than v? InputThe first line contains an integer t that is the number of experiments
(1 ≤ t ≤ 1000). Then the description of the experiments follows,
each of them is described by a block of four lines. The first line of each block contains integers v and a
(1 ≤ v ≤ 50 000; 1 ≤ a ≤ 1000).
Each of the following three lines contains integers xi, yi, zi,
which are the coordinates of the point Oi
(−106 ≤ xi, yi, zi ≤ 106; x12 + y12 > 0).
It is guaranteed that the magion’s path won’t have a horizontal arc
it will follow with the speed exactly v. OutputFor each experiment output in a separate line the overall length of the magion’s path segments
where its speed is not less than v.
The answers should be output with an absolute of relative error not more than 10−6. Sample
NotesThere is one experiment in the example. The path looks the following way: from point (0,0,0) to point (4,0,2): an arc with measure equal to arcsin(0.8) of the circle with the radius 5; from point (4,0,2) to point (20,16,2): a quarter of the circle with the radius 16; from point (20,16,2) to point (20,16,2): a full circle with the radius 1. Problem Author: Denis Dublennykh (prepared by Eugene Kurpilyansky) Problem Source: NEERC 2014, Eastern subregional contest Tags: geometry hardest problem |
