| ENG RUS | Timus Online Judge |
1560. Elementary Symmetric FunctionsTime limit: 4.0 second Memory limit: 64 MB In this task, you are to read an array of integer numbers (A[1..N]) and a sequence
of M queries of two types:
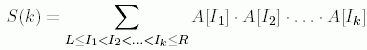 You should compute their values modulo prime P.
InputThe first line consists of three integer numbers: N (size of the array), M (number of queries) and P (prime number)
(1 ≤ N ≤ 80000; 1 ≤ M ≤ 100000; 1000 ≤ P ≤ 109 (prime)).
The second line contains N integer numbers not exceeding 105 by absolute value (the initial values in the array).
The next M lines contain queries. Each query can be either increase or calculation query. I index delta — increase index-th value by delta (1 ≤ index ≤ N; −105 ≤ delta ≤ 105).
C left right K — compute S(0), …, S(K) for the interval [left..right] (1 ≤ left ≤ right ≤ N;
1 ≤ K ≤ 4; K ≤ right − left + 1).
All fields in each line are separated by spaces.
OutputFor each calculation query print a line consisting of K + 1 numbers — S(0) S(1) … S(K).
These numbers must be nonnegative and less than P.
Sample
Problem Source: Novosibirsk SU Contest. Petrozavodsk training camp, September 2007 Tags: data structures number theory |
