| ENG RUS | Timus Online Judge |
1814. Continued FractionTime limit: 0.5 second Memory limit: 64 MB It is known that any irrational number d greater than 1 can
be represented as infinite continued fraction:
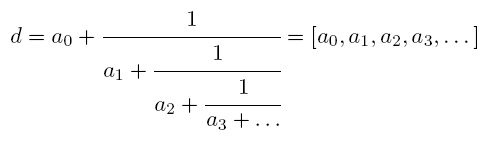 Here ai are positive integers. A convergent fraction of order k of number d is a rational number [a0, a1, …, ak], that is a representation of d as a continued fraction, truncated to the first k + 1 elements. Given an integer x, find numerator and denominator
of convergent continued fraction of order k of the square root of x. InputThe only input line contains integers x and k
(2 ≤ x ≤ 106; 0 ≤ k ≤ 109). x is not a perfect square. OutputOutput the value of the convergent continued fraction of order k of the square root of x as an irreducible fraction. Output numerator and denominator modulo 109 + 7. Sample
Problem Source: Tavrida NU Akai Contest. Petrozavodsk Summer Session, August 2010 Tags: none |
