| ENG RUS | Timus Online Judge |
2166. Two RoadsTime limit: 3.0 second Memory limit: 256 MB Many people have heard of Yandex.Go, but few know about the new secret development called Yandex.GoRod, which will help in the construction of new cities. The application will represent the future city as a plane with Cartesian coordinates. At this stage, N railway tracks have already been laid out as infinite straight lines, with a station located at each intersection. For convenience sake, the city center is located at the origin, and roads can only be built parallel to the coordinate axes. Naturally, it is necessary to connect the city center with each planned station. It is easy to guess that this will require no more than two roads: one horizontal and one vertical. However, it is more difficult to understand how much money will be spent on this. It is known that one kilometer of road costs one million rubles. To start with, it was decided to connect the city center with the station that requires the most expensive roads. Help the developers of the Yandex.GoRod application implement a function that finds this cost. InputThe first line contains an integer N — the number of railway tracks (2 ≤ N ≤ 105). The next N lines describe these railway tracks with four integers x1i, y1i, x2i, y2i — the coordinates of two different points through which the line containing the railway track passes. All coordinates are given in kilometers and do not exceed 1000 in absolute value. It is guaranteed that there are no parallel lines in the input. OutputOutput the maximum cost of connecting the city center with a station using no more than two roads parallel to the coordinate axes, in millions of rubles. The answer will be accepted if the absolute or relative error of the values does not exceed 10−4. Formally, let your answer be x, and the jury’s answer be y. Your answer will be considered correct if |x−y| / max(1,|y|) ≤ 10−4. Sample
NotesIllustration for the example (the first, second, and third roads are denoted as a, b, and c respectively):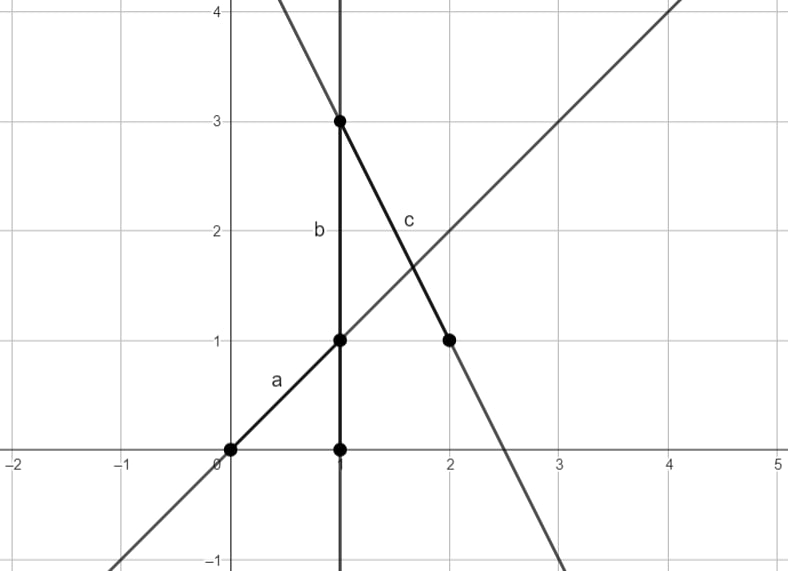 Problem Author: Vadim Barinov Problem Source: Ural School Programming Contest 2022 Tags: geometry |
