| ENG RUS | Timus Online Judge |
УрКОП 2020
Contest is over
H. Flight on a CannonballTime limit: 2.0 second Memory limit: 256 MB Baron Munchausen is participating in a battle. It’s occurring on a plane with a Cartesian coordinate system. He is ordered to move to the center of the coordinate system. It’s quite simple to do: he just needs to mount a cannonball and jump off of it as close to the center as possible. There are n cannons on the battlefield, Munchausen is near one of them. Cannons are considered as points, i-th point has coordinates (xi, yi). Being near one of the cannons, Baron can shoot in the direction of any other cannon and mount the cannonball. He cannot miss the cannon: that would damage his reputation. The cannonball flies in a straight line and never stops, even after reaching the targeted cannon. Flying over any cannon, Munchausen can dismount the cannonball and shoot in the direction of any other cannon again. This way he can freely move from cannon to cannon. When Baron decides that he is close to the center of the coordinate system, he will dismount the cannonball and walk to the center on foot. Find the smallest possible distance Baron Munchausen would need to walk on foot. InputThe first line contains one integer n (2 ≤ n ≤ 105) — amount of cannons. Next n lines each contain two integers xi and yi (−105 ≤ xi, yi ≤ 105) — coordinates of a cannon. It is guaranteed that no two cannons are located at the same point. OutputOutput one real number — the smallest possible distance that Baron Munchausen will walk by foot after traveling by cannonballs. Your answer is considered correct if its absolute or relative error doesn’t exceed 10−6. Samples
NotesIllustration of the second example: 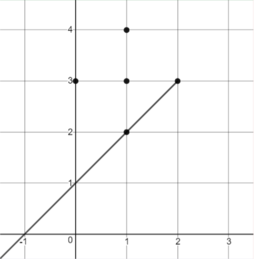 Problem Author: Valentin Zuev Problem Source: Ural School Programming Contest 2020 |
