| ENG RUS | Timus Online Judge |
Ural Championship 2008
Contest is over
C. CactusesTime limit: 1.0 second Memory limit: 64 MB There is no doubt that Yekaterinburg trams are the best in the world.
Nevertheless, it is Saint-Petersburg that has the largest tram network in
Russia. Not long ago, the Saint-Petersburg tram network was included into the
Guinness Book of Records as the largest in the world. Two fans of the tram forum from Yekaterinburg decided to make a trip to
Saint-Petersburg to visit the centenary celebration of the tram launch in that
city. From their Saint-Petersburg friends they learned that in the previous 15
years the amount of tram service had been constantly decreasing. In many
avenues, tram lines were dismantled. Tram service in the city center was
minimized, and the city tram network was divided into three fragments, so that
it was no longer possible to get by tram from any part of Saint-Petersburg to
any other part. 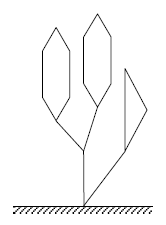 Another thing the travelers learned was that cactuses were in fashion in
Saint-Petersburg. Upon their return to Yekaterinburg, they decided to plant a
cactus at their office. A cactus is a connected undirected graph such that each
of its edges belongs to at most one simple cycle. One vertex of a cactus
touches the ground and is called its root. However, it soon turned out that cactuses became too popular, and all fans
of the tram forum already had them. Then the friends decided to get rid of
their cactus by a very unusual method: they by turns choose some edge of the
cactus and chop it up. This edge is removed, and if the cactus breaks into two
parts, then the part that is not connected to the root anymore is thrown out. The friends have bet a monthly tram ticket on who will chop the last edge
growing from the root. Determine who will win if they both play optimally. InputAlong with the vogue of cactuses, the friends follow
the Saint-Petersburg vogue to describe the set of edges of a cactus by a family
of paths such that in each path all edges are different. The first line
contains the amount n of vertices of the cactus, the amount m of
paths, and the number r of the root vertex; 1 ≤ r ≤
n ≤ 50000. lines describes a path in the form of a
sequence of its vertices. Each description starts with the length of the
sequence ni (2 ≤ ni ≤ 100000). Then
there are ni integers, which are the numbers of vertices of
the path, in the order in which they are on the path. Adjacent vertices of any
path are different. There can be at most one edge between any two vertices of
the cactus. Each edge of the cactus is given in the input only once. OutputOutput “First” if the person who makes
the first move wins a monthly ticket assuming that both play optimally.
Otherwise, output “Second”.
Samples
Problem Author: Alexander Ipatov, Vladimir Yakovlev Problem Source: The 12th Urals Collegiate Programing Championship, March 29, 2008 |
