| ENG RUS | Timus Online Judge |
Уральская региональная командная олимпиада по программированию 2019
Соревнование завершено
K. Безумный выстрелОграничение времени: 0.5 секунды Ограничение памяти: 256 МБ Шер безумно любит играть в одну известную браузерную io-игру. Играя в неё каждый день, Шер добился больших результатов, и теперь он даже состоит в сильнейшем СНГ клане по ней. Игра эта представляет собой 2D Battle Royale (Королевская битва). Поле сражения представляет собой координатную плоскость с расположенными на ней зданиями, камнями, деревьями, бочками, кустами, мостами и реками, а так же металлическими цистернами. Высшим скиллом в игре считается меткая стрельба из снайперских винтовок. И Шер, конечно же, уже хорошо освоил этот навык. От нечего делать, он решил выработать в себе новый навык, суть которого заключается в меткой стрельбе по врагам через поверхности, которые отражают пули. В данной игре такими поверхностями являются все металлические поверхности. На экране игрока этот навык выглядит примерно так, как на картинке. В данный момент Шер обнаружил удобный случай для демонстрации своей меткости: он заметил на карте цистерну и противника. Помогите Шеру поразить цель новым навыком, выведите координаты точки на цистерне, в которую ему необходимо выстрелить. Выстрел по касательной, не изменяющий траекторию пули, не считается демонстрацией скилла. Для простоты задачи будем считать, что на карте нет ничего, кроме цистерны, имеющей формы круга, и двух равноудалённых от неё игроков, которых мы будем представлять как материальные точки, а также считать, что угол падения пули равен углу отражения. 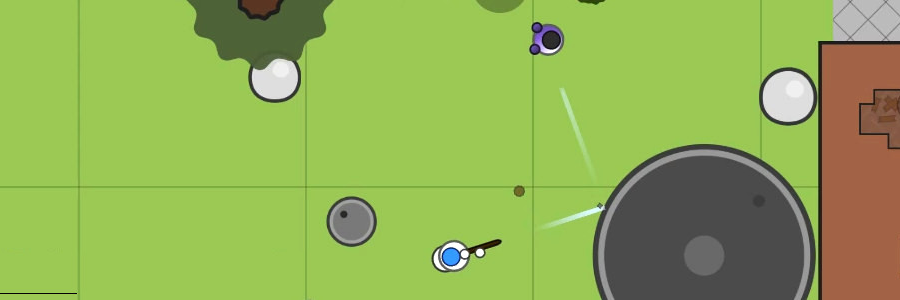 Исходные данныеВ первой строке даны три целых числа через пробел — координаты центра и радиус цистерны (всегда положительный). Во второй строке даны два целых числа через пробел — координаты Шера. В третьей строке даны два целых числа через пробел — координаты противника. Все числа целые, по модулю не превосходящие 3000. Гарантируется, что местоположения Шера и его противника различны и находятся за пределами цистерны. Гарантируется, что расстояния от Шера и противника до центра цистерны одинаковые. РезультатЕсли требуемой точки не существует, в единственной строке выведите « No way» (без кавычек). Иначе, в единственной строке выведите два числа через пробел — ответ на задачу. Ответ будет засчитан, если расстояние от точки до центра цистерны отличается от радиуса не более, чем на 10−6, угол падения отличается от угла отражения не более, чем на 10−6, и траектория выстрела не содержит внутренних точек цистерны. Если возможных точек несколько, выведите любую.Примеры
Автор задачи: Кирилл Мещеряков Источник задачи: Уральская командная олимпиада по программированию 2019 |
