| ENG RUS | Timus Online Judge |
Ural SU contest. Petrozavodsk training camp. Summer 2010
Contest is over
E. Integer-valued Complex DeterminantTime limit: 1.0 second Memory limit: 64 MB A Gaussian integer is a complex number with integer components.
If a, b, q, r are Gaussian integers, a = bq + r, and |r| < |b|, then r
is a remainder of division of a by b. Let p be a Gaussian integer and X = (xij) be a matrix of size n × n where all xij are Gaussian integers too. Your goal is to calculate the remainder of division of determinant of X by p. Remember, that the determinant of X
is equal to 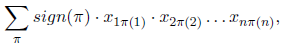 where the summation is taken over the set of all permutations of n elements.
Here addition and multiplication are the usual addition and multiplication of complex numbers. InputThe first line contains an integer n (1 ≤ n ≤ 50). Each of the next n lines contains n space-separated complex
numbers which are the elements of X. The last line contains a non-zero complex number p. Complex number is denoted by
its real and imaginary parts, separated with space. All components of all complex numbers don't exceed 10 000 in their absolute value. OutputOutput real and imaginary parts of the remainder of division of determinant of X by p.
If there are several possible answers, output any of them. It is guaranteed that the answer exists. Sample
Problem Author: Dmitry Poletaev, Ivan Burmistrov Problem Source: Ural SU Contest. Petrozavodsk Summer Session, August 2010 |
